
/* 본 게시물은 ' 파이썬 라이브러리를 활용한 데이터 분석 2판 | with 웨스 맥키니 ' 의 내용과 참고자료를 토대로 작성되었습니다. */
/* 본 글은 개인적으로 공부한 내용을 정리한 글이므로 오류가 있을 수 있습니다. */
난수 생성
Numpy.random 모듈
numpy.random 모듈은 파이썬 내장 random 함수를 보강하여 다양한 종류의 확률분포로부터 효과적으로 표본값을 생성하는데 주로 사용된다.
표본정규분포 표본 생성
randomData = np.random.normal(size=(4,4))
print(randomData)
"""
[[ 5.96710372e-01 -5.86135000e-01 1.19199216e-01 -1.90140372e+00]
[ 9.86277664e-01 3.92835287e-01 -4.99643703e-02 -4.01555594e-01]
[ 1.90872305e+00 -4.39362316e-01 1.78006844e+00 1.33969665e+00]
[ 1.17523403e+00 2.17271801e+00 5.95404338e-01 1.17560283e-03]]
"""
random vs numpy.random 생성 시간비교
n = 1000000
start = time.time()
randomDataByRandom = [normalvariate(0,1) for _ in range(n)]
end = time.time()
print("{0}".format(end - start))
start = time.time()
randomDataByNumpy = np.random.normal(size = n)
end = time.time()
print("{0}".format(end - start))
위 결과를 통해 numpy.random 모듈은 매우 큰 표본을 생성하는데 파이썬 내장 모듈보다 수십 배 빠르다는 것을 알 수 있다. 이러한 차이가 발생하는 이유는 난수 생성기의 시드값에 따라 정해진 난수를 알고리즘으로 생성(유사난수)하기 때문이다. Numpy 난수 생성기의 시드값은 np.random.seed를 이용해서 변경할 수 있다.
격리된 난수 생성기
일반적으로 numpy.random 에서 제공하는 데이터를 생성할 수 있는 함수들은 전역 난수 시드값을 이용한다. numpy.random.RandomState를 이용해 다른 난수 생성기로부터 격리된 난수 생성기를 만들 수 있다.
rng = np.random.RandomState(1234)
dataByRandomState = rng.randn(10)
print(dataByRandomState)numpy.random 함수
| 함수 | 설명 |
| seed | 난수 생성기의 시드를 지정한다. |
| permutation | 순서를 임의로 바꾸거나 임의의 순열을 반환한다. |
| shuffle | 리스트나 배열의 순서를 뒤섞는다. |
| rand | 균등분포에서 표본을 추출한다. |
| randint | 주어진 최소/최대 범위 안에서 임의의 난수를 추출한다. |
| randn | 표준편차가 1이고 평균값이 0인 정규분포에서 표분을 추출한다. |
| binomial | 이항분포에서 표본을 추출한다. |
| normal | 정규분포에서 표본을 추출한다 |
| beta | 베타푼포에서 표본을 추출한다. |
| chisquare | 카이제곱분포에서 표본을 추출한다. |
| gamma | 감마분포에서 표본을 추출한다. |
| uniform | 균등 [0,1) 분포에서 표본을 추출한다. |
Numpy.random 예제 (계단 오르내르기)
계단에서 같은 확률로 한 계단 올라가거나 내려가는 시행을 1000번 테스트해보자.
순수 파이썬의 random 사용
파이썬의 random 모듈을 사용하면 다음과 같이 코드를 작성할 수 있다.
import random
import matplotlib.pyplot as plt
position = 0
walk = [position]
steps = 1000
for i in range(steps):
step = 1 if random.randint(0,1) else -1
position += step
walk.append(position)
plt.plot(walk[:100])
plt.show()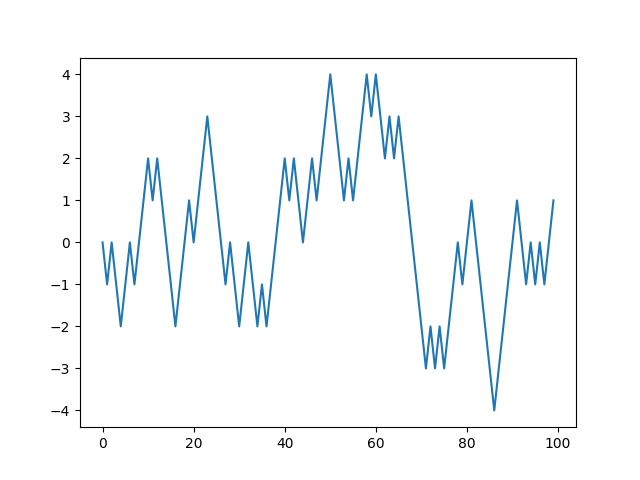
Numpy.random 사용
draws = np.random.randint(0, 2, size=steps)
steps = np.where(draws > 0, 1, -1) # where(조건, if true , if false) -> 양수는 1로 0는 -1로
walk = steps.cumsum()
print(walk) # 과정확인
print(steps.sum()) # 최종 결과
print(walk.min()) # 최솟값
print(walk.max()) # 최댓값한번에 시뮬레이션하기
위 테스트를 2000번 진행할 때 효율적으로 처리할 수 있는 방법에 대해 알아보자.
# 한번에 시뮬레이션하기 시행횟수 늘리기
nwalks = 2000
nsteps = 1000
draws = np.random.randint(0,2, size=(nwalks, nsteps)) # 0 또는 1
steps = np.where(draws > 0, 1, -1)
walks = steps.cumsum(1)
print(walks)방법은 간단하다. 2차원 배열로 2000 x 1000 size 의 randint 배열을 생성하면된다. cumsum(1) 은 row 의 합 과정을 보여준다.
특정 시점 계산
중간에 한 번이라도 계단의 20 지점까지 도달한 경우만 추출하는 방법에 대해 알아보자.
hits20 = (walks >= 20).any(1) # any()메서드를 사용해서 20을 도달 or 넘었는지 확인
print(hits20) # 한 번이라도 20에 도달하면 True, 아니면 False 반환
print(hits20.sum()) # 20을 넘는 경우의 수
print(walks[hits20]) # 20이 넘는 행만 가져옴
참고 자료
[URL] :




