
참고 자료
[BoostCourse - 모두를 위한 컴퓨터 과학 (CS50 2019) - 알고리즘] : https://www.boostcourse.org/cs112
#Big-O
최근 들어 코드를 짜다보면 '조금 더 효율적(좀 더 빠르게)으로 만들 수 있지 않을까?' 라는 생각을 많이 한다. 그래서 조금 더 효율적인 코드들을 쓰는 방법에 대해 배우고자 한다. 간단한 CS 내용들부터 정리하고 차례차례 알고리즘에 대해 공부해 나가보자.
우리가 프로그램을 작성한 후에 실행하면 작업이 완료될 때 까지 어느정도 시간이 소요된다. 아주 간단한 프로그램인 경우에는 걱정할 필요가 없지만, 처리하는 데이터가 많아지고 처리하는 작업이 복잡해질수록 실행 시간은 매우 중요해진다. 특정 알고리즘을 작성하였을 때 그 실행 시간을 표기하는 방법을 배워보자.
1. 알고리즘이란?
우선, 위키백과에서 알고리즘을 검색해보았다.
알고리즘은 수학과 컴퓨터과학, 언어학 또는 엮인 분야에서 어떠한 문제를 풀어맺기 위해 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것, 계산을 실행하기 위한 단계적 절차를 의미한다. 즉, 문제풀이에 필요한 계산절차 또는 처리과정의 순서를 뜻한다. 프로그램명령어의 집합을 의미하기도 한다.
[출처] : 위키백과 - 알고리즘
https://ko.wikipedia.org/wiki/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
결국 알고리즘이란 문제를 푸는 방법이라고 생각하면된다.
그렇다면 좋은 알고리즘이란 무엇일까?
다음은 좋은 알고리즘의 특징이다.
- 정밀성 : 변하지 않는 명확한 작업 단계를 가져야 한다.
- 유일성 : 각 단계마다 명확한 다음 단계를 가져야 한다.
- 타당성 : 구현할 수 있고 실용적이어야 한다.
- 입력 : 정의된 입력을 받아들일 수 있어야 한다.
- 출력 : 답으로 출력을 내보낼 수 있어야 한다.
- 유한성 : 특정 수의 작업 이후에 정지해야 한다.
- 일반성 : 정의된 입력들에 일반적으로 적용할 수 있어야 한다.
내가 생각하는 좋은 알고리즘이란 걸리는 시간이 최대한 짧아야 되고, 가독성이 좋고, 정확하게 문제를 처리하는 것이다. 추가적으로 범용성도 고려해야할 것이다.
이번 시간에는 걸리는 시간에 대한 알고리즘 평가 방법인 시간 복잡도에 대해 알아보자.
2. 시간 복잡도란?
알고리즘을 평가하는 대표적인 방법 중 하나인 시간 복잡도이다. 시간 복잡도란 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가르킨다. 컴퓨터과학에서 알고리즘의 시간복잡도는 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것이다. 알고리즘의 시간복잡도는 주로 빅-오 표기법을 사용하여 나타낸다.
3. Big - O 표기법
Big-O 표기법은 어떤 알고리즘을 실행했을 때 최악의 상황을 가정하여 걸리는 시간을 표현한다. 즉, Big-O 는 실행 시간의 상한을 나타낸다. (다른 표기법으로 실행 시간의 하한을 나타내는 Big-Ω 도 있다.)
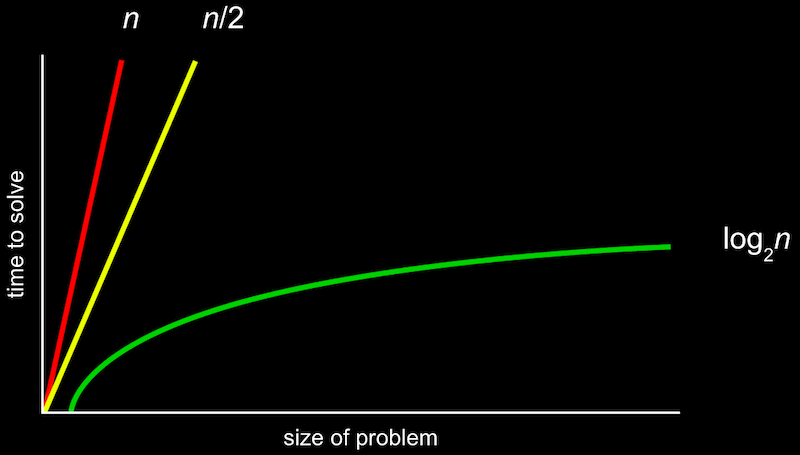
위와 같은 그래프를 공식으로 표기한 것이 Big-O 표기법이다. 여기서 O는 "on the order of"의 약자로, 쉽게 생각하면 "~만큼의 정도로 커지는" 것이라고 볼 수 있다.
위 n 그래프와 n/2 그래프를 보자. 위 두 그래프를 Big-O 표기법으로 표현하면 O(n)이다. O(n)은 n만큼 커지는 것이므로 n이 늘어날 수록 선형적으로 증가한다. n이 계속해서 커지면 1/2은 큰 의미가 없어지므로 둘 다 O(n)이다. (극한으로 생각하면 좀 더 쉽게 이해할 것이다.)
Big O 를 극한의 개념으로 바라보면 Big O의 특징을 알 수 있다. Big O는 계수와 낮은 차수의 항을 제외시킨다.
예시로서, 만약 크기 n의 모든 입력에 대한 알고리즘에 필요한 시간이 최대 (어떤 n0보다 크지 않은 모든 n에 대하여) 5n3 + 3n+ 2의 식을 가진다면, 이 알고리즘의 점근적 시간 복잡도는 O(n^3)이라고 할 수 있다.
위의 예시를 통해 영향력이 낮은 항과 상수항을 무시하는 규칙을 알 수 있다.
다음으로 대표적인 Big-O를 알아보자.
주로 아래와 같은 Big-O 표기가 실행 시간을 나타내기 위해 많이 사용된다.
- O(n^2)
- O(n log n)
- O(n) - 선형 검색
- O(log n) - 이진 검색
- O(1)
O(n)의 간단한 예시를 들어보겠다.
for(int i=0; i<n; i++) {
println(n);
}반복문을 통해 n번 반복되었으므로 Big-O 표기법으로 O(n)이라 나타낼 수 있다.
그렇다면 이중 반복문은? 반복문이 두 번 겹쳐져 있으므로 O(n^2)으로 나타낼 수 있다.
이외에도 O(nm), O(2^n) 등 많은 Big O가 있다. 선형 검색과 / 이진 검색에 대한 내용은 검색 알고리즘 글에서 정리하겠다.
2021/8/25 - 1일 1알고리즘 공부 시작




