
이번 게시글에서는 적합한 회귀모형을 평가하는 방법인 `회귀 진단`에 대해 알아보겠습니다.
회귀진단의 목표는 다음과 같습니다.
- 모형이 얼마나 데이터 상황을 잘 설명하는지 확인
- 모형에 대한 각 데이터의 영향에 대해 확인
data <- datasets::mtcars
model <- lm(mpg~disp+hp+wt+drat, data=mtcars)
summary(model)- 사용한 데이터는 R 내장 데이터인 mtcars입니다.
- mtcars는 32가지 차종에 대한 특성 변수들로 구성되어 있습니다.
- 반응 변수(타겟값)로 mpg를 설명 변수로는 수치형 데이터인 dsip, hp, wt, drat를 사용하여 다중회귀선형모형을 적합했습니다.
영향점 진단
- `영향점` : 어떤 특정 관측값이 있을 때와 그것을 제외했을 떄 적합된 회귀함수에 큰 차이가 생기는 경우
- 즉, 회귀 모수 추정에 영향을 주는 점
- 영향점을 판단하는 기준 : `모자행렬`, `Cock’s Distance`, `DFFITS`, `추가 변수 그림`
스튜던트화 잔차
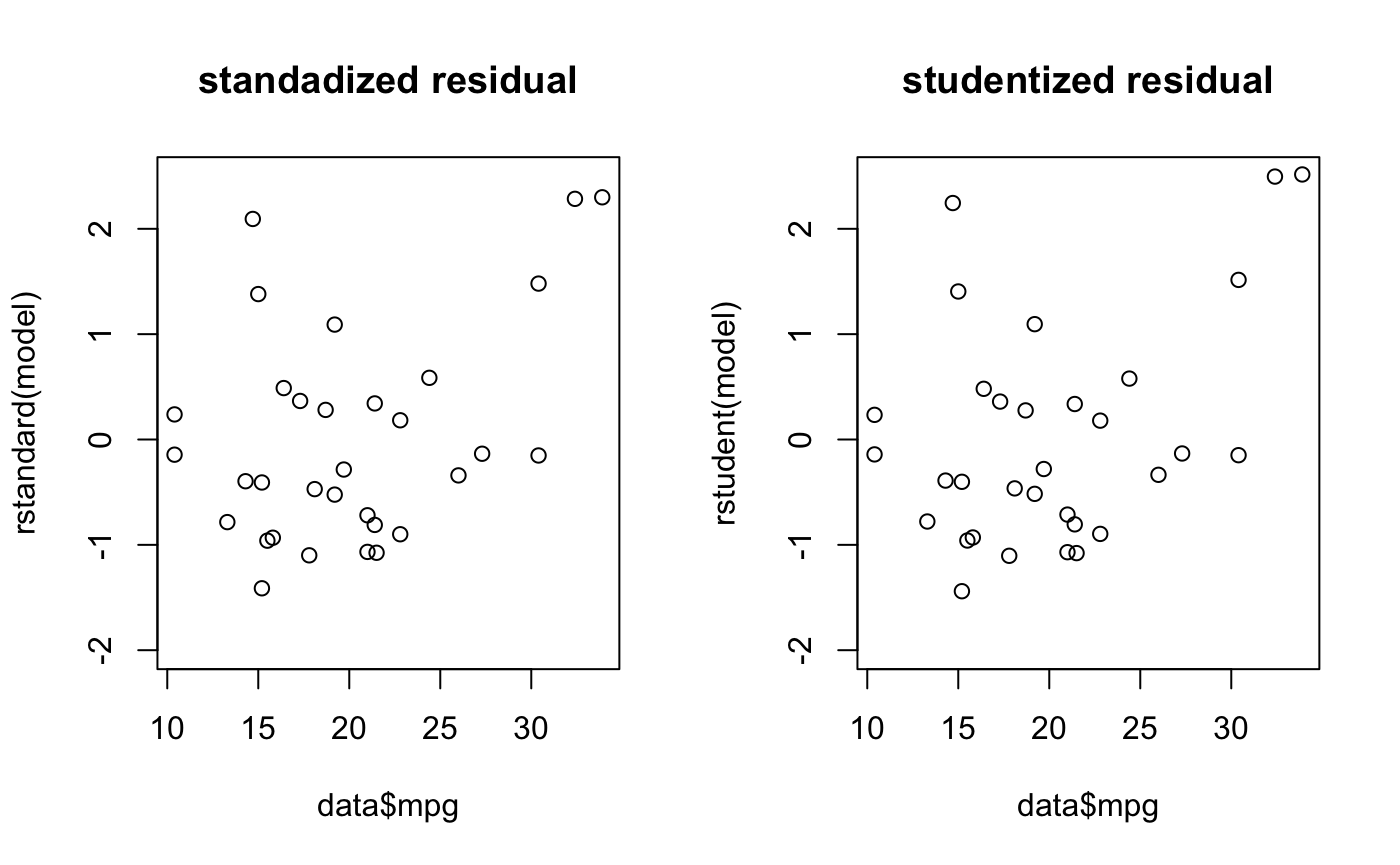
우선, 스튜던트화 잔차를 확인해보겠습니다.
par(mfrow=c(1,2))
rstandard(model)
rstudent(model)
plot(data$mpg, rstandard(model), ylim=c(-2,2.5), main="standadized residual") # 스튜던트화 잔차
plot(data$mpg, rstudent(model), ylim=c(-2,2.5), main="studentized residual") # 스튜던트화 제외잔차- 스튜던트화 잔차 종류
- rstandard() : 내적 스튜던트화, 잔차를 표준오차로 나눈 값. rstudent와 달리 i번째 값을 포함한다.
- rstudent() : 외적 스튜던트화, i번째 값 제거 한 rstandard 값
- 내적, 외적 스튜던트화 값의 차이가 미비해 보인다. 단, 극단값에 대해서는 약간의 차이가 존재한다.
Cock's Distance
- `Cock’s Distance` : i 번째 관측이 n개의 적합값 전체에 미치는 영향의 척도, 즉 각각의 값이 얼마나 많이 회귀 모델을 변화시키는지 확인할 수 있다.
- i 번째 데이터가 없을 때(n-1)와 비교하여 차이가 많이나면 이상점으로 판단한다.

thresold <- 4/((nrow(data)-length(model$coefficients)-2))
thresold # 0.16
plot(model, which=4, cook.levels = thresold)$$\frac{4}{\text{자유도}} = \frac{4}{\text{n-k-2}} $$
- Cook's 거리의 임계값은 일반적으로 위와 같습니다. 여기서 자유도는 데이터의 행 수에서 모델의 계수 수(k+1, k: 설명변수 개수)와 상수항에 2를 뺀 값입니다.
- which=4는 Cook's 거리를 나타내는 그림을 생성하라는 옵션입니다. Cook's 거리 그림은 모델에서 한 데이터 포인트가 다른 데이터 포인트에 미치는 영향을 시각화합니다.
DFFITS
- `DFFITS` : i번째 값 포함 미포함에 따른 fitted value값의 변화량, 쿡의 거리 측도 변형 형태
$$2 \sqrt{\frac{(k+1)}{n}}$$
일반적으로 DFFITS의 절댓값이 위 값보다 큰 경우 영향점이라 판단합니다.
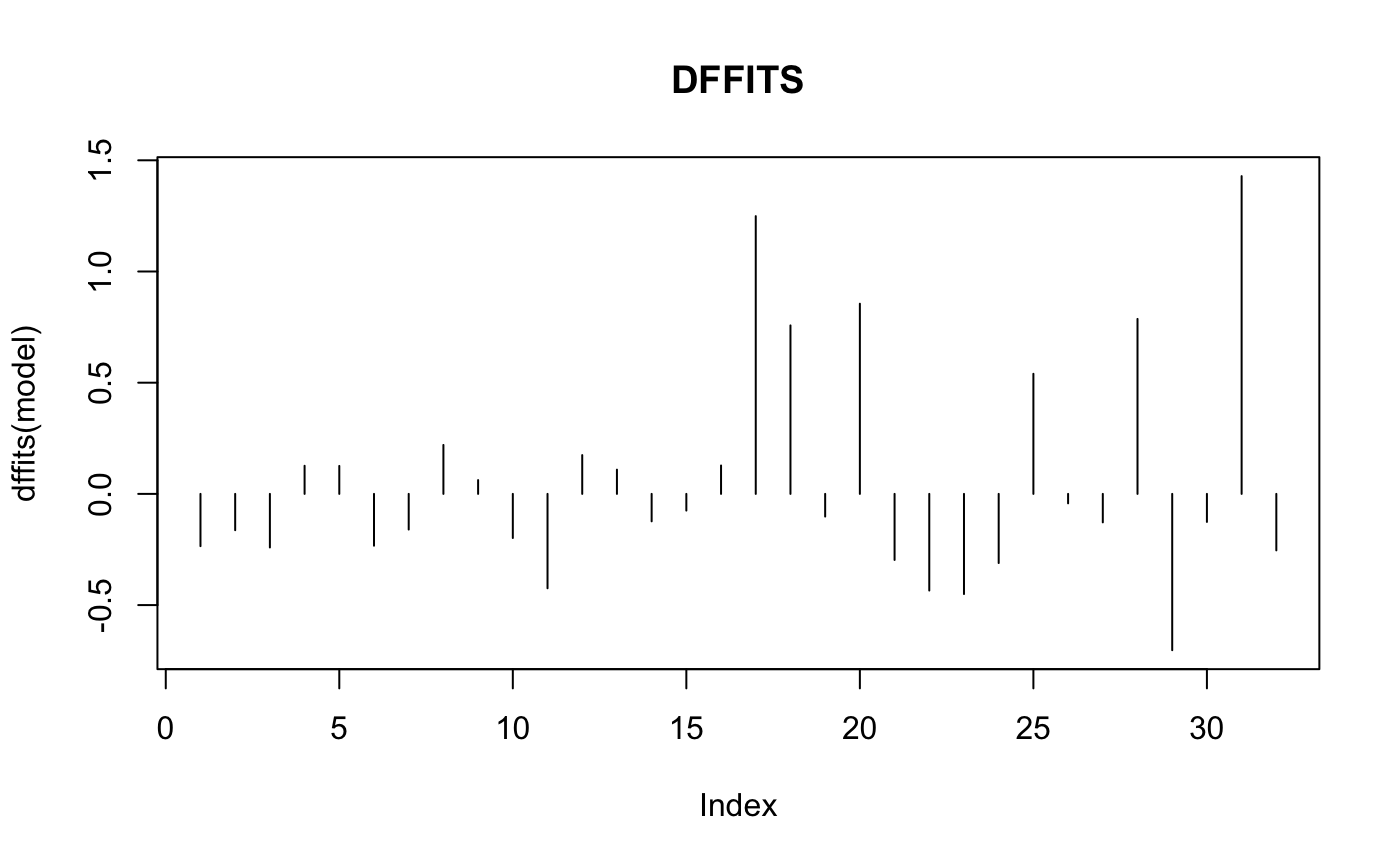
dffits(model)
plot(dffits(model), type="h", main="DFFITS")추가 변수 그림

library(car)
avPlots(model) # added variable plot- `car` 라이브러리의 `avPlots()`을 이용하여 추가 변수그림을 확인할 수 있다.
influence()
R의 `influence` 함수로 각 회귀진단 통계량에 따른 영향점을 찾을수 있습니다.

influence.model <- influence.measures(model)
summary(influence.model)
- 영향점 가능성이 높은데이터를 출력합니다.
- `dfb`는 "difference in fits, beta-weighted"의 약어로, 회귀 분석에서 모델의 피팅 값 간의 차이를 나타내는 값입니다. dfb 값은 특정 변수의 영향력을 의미합니다. 이는 Cock's distance 를 계산할때 사용합니다.
- * 로 영향점 기준이 넘는 값을 표시해줍니다.
또한, 회귀진단 통계량은 `ls.diag()`을 통해 확인할 수 있습니다.
ls.diag(model)추가로 영향점인 점의 index를 출력해보겠습니다.

# influence.model$is.inf
# apply(influence.model$is.inf, 1, any)
which(apply(influence.model$is.inf, 1, any))
이상점 진단
- `이상점` : 나머지 값들과 동떨어져 있는 특정 관측값 (outlier)
- 이상점은 잔차의 절댓값 ei 이 매우 큰 경우가 될 수 있으나 잔차 절댓값이 크다고 항상 이상점이 되는 것은 아니다.
- 이상점 검정을 통해 이상점을 찾을 수 있다.
이상점은 car 라이브러리의 `outlierTest()` 로 찾을 수 있다.

outlierTest(model)- Toyaota Corolla를 이상점으로 찾았습니다.
참고자료
[1] 오차와 잔차, 표준화 잔차
[2] 이상값 진단
반응형




